| advertisement: compare things at compare-stuff.com! |
We have tried to use self-organising maps to filter sequences of residue
properties, such as hydrophobicity, using three dimensional structure
information. The output most closely resembles the input where the
input sequence properties are clustered in three dimensional space, and
is smoothed where they are not. The mapped (or filtered) sequences
should describe the essence of the fold in terms of the properties used.
In other words, self-organised sequence property `fields' are generated
within the structure. In order to test how well this abstraction could
describe the common features of distantly homologous and analogous
folds, the structure-mapped sequences were used in fold recognition
trials. Their poor performance in this task was probably due to the
loss or corruption of detailed magnitude information in the property
vectors. An approach is needed whereby during the alignment
structurally relevant information is aligned more stringently than
structurally irrelevant information. One way to achieve this is to
align the query sequence with unmapped library sequences which have been
masked in some way according to how well the residue property vectors
map. This can be measured by the quantisation error
(Equation 5.3), ![]() , which is large when the input vector
, which is large when the input vector
![]() represents a residue with structurally anomalous properties. One
could also set position specific gap penalties based on
represents a residue with structurally anomalous properties. One
could also set position specific gap penalties based on ![]() . Both
approaches might be equivalent to the already common use of secondary
structure dependent gap penalties[Barton & Sternberg, 1987]. This
highlights the major limitation of the approach, at best we can hope to
create a field of hydropathy for library folds and/or define
core/non-core residues.
. Both
approaches might be equivalent to the already common use of secondary
structure dependent gap penalties[Barton & Sternberg, 1987]. This
highlights the major limitation of the approach, at best we can hope to
create a field of hydropathy for library folds and/or define
core/non-core residues.
If somehow these ideas could be transformed into a true threading
method, taking into account the three-dimensional interactions of query
residues placed `inside' the library fold, further progress might be
made. By creating maps of structure, sequence properties and
sequence position (distance along the chain), it would be possible to
perform a double dynamic `structural' alignment using the map of the
library sequence and structure. For example, pairwise vectors ![]() and
and
![]() could be compared in a low level alignment to determine
could be compared in a low level alignment to determine ![]() in a similar way to SSAP. The vector
in a similar way to SSAP. The vector ![]() would be a two dimensional
vector between the map nodes corresponding to the mapping of input
vectors
would be a two dimensional
vector between the map nodes corresponding to the mapping of input
vectors ![]() and
and ![]() respectively. Vector
respectively. Vector ![]() would be likewise
defined. The input vectors for these mappings
would be likewise
defined. The input vectors for these mappings ![]() ,
, ![]() ,
, ![]() and
and
![]() are defined below. Their components, in order, are carbon-
are defined below. Their components, in order, are carbon-![]() coordinates (
coordinates (![]() ,
, ![]() ,
, ![]() ) and component(s) of the sequence property
vector (
) and component(s) of the sequence property
vector (![]() ).
).
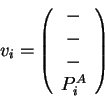 |
(16) |
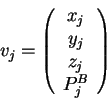 |
(17) |
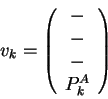 |
(18) |
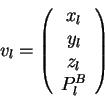 |
(19) |
Dashes indicate that the atomic coordinates are not used to find the
closest map vector. In the mapping of query sequence input vectors
![]() and
and ![]() using the library sequence-structure map, the sequence
property vectors should contain sufficient information to direct the
mapping in the absence of three dimensional information. Such
information could include separate components of hydrophobicity,
conservation and secondary structure prediction as already discussed,
and one dimensional sequence position (with a low weighting) might also
help.
using the library sequence-structure map, the sequence
property vectors should contain sufficient information to direct the
mapping in the absence of three dimensional information. Such
information could include separate components of hydrophobicity,
conservation and secondary structure prediction as already discussed,
and one dimensional sequence position (with a low weighting) might also
help.
Another approach might be to use self-organising maps in a completely different way to generate multiple sequence/profile based distance potentials for threading, which cannot currently be represented algorithmically[Taylor, 1997]. The implementation would be slow, because using the mapping to generate preferred distances from pairs of profiles would involve a complete search of the potential map instead of the quickly accessed array implementation of single sequence distance potentials. Testing on a few alignments would be feasible however, and processing power will inevitably increase to make full library searches possible. A similar, and possibly faster approach could be to use feed-forward neural networks, trained on pairs of profiles with known distance separations.
Self-organising maps have not been shown here to improve alignments using structural information. This work has, however, shown that the self-organising principle has interesting potential in sequence and structural studies.