advertisement: compare things at compare-stuff.com!

Accessibility and burial

Solvent accessible surface area was calculated using the algorithm of Lee and Richardslee:sa as implemented in the program access by Simon Hubbard (unpublished). We used the probe contact surface area in preference to the probe centre locus surface (see Figure 1.2), and a probe of radius 1.4Å. Accessible contact surface areas ($a.c.s.a.$) are smaller than probe locus surfaces and molecular surfaces by a factor of approximately 3.4 and 2.8 respectively.

An accessible residue is defined as having an $a.c.s.a > 1.0$Å$^2$. An antigen contacting residue is defined by burial from solvent by antigen binding such that

$$\Delta^{u}_{c}~a.c.s.a > 1.0\mbox{\AA}^2$$

where

$$\Delta^{u}_{c}~a.c.s.a = a.c.s.a_{uncomplexed} - a.c.s.a_{complexed}.$$

Fraction burial per residue for residue $r$, $\rho_{r}$, is defined as the fraction of solvent accessible surface area buried by antigen.

$$\rho_{r} = \frac{\Delta^{u}_{c}~a.c.s.a}{a.c.s.a_{uncomplexed}}$$

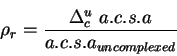
Mean fraction burial, $\overline{\rho}$, at residue $r$ is defined as

$$\overline{\rho}_{r} = \frac{1}{N} \sum_{a=1}^{N} \rho_{r}$$

where $N$ is the number of antibody structures possessing a solvent accessible residue $r$ ($a.c.s.a>0$).