| advertisement: compare things at compare-stuff.com! |
For each type of domain ![]() at a given level in the CATH classification
(e.g. class, architecture), and amino acid or duplet type
at a given level in the CATH classification
(e.g. class, architecture), and amino acid or duplet type ![]() (from now on
referred to as a pattern) the number of observations
(from now on
referred to as a pattern) the number of observations ![]() in the
dataset are counted. The counts from multiple sequences are averaged and
rounded down. The number of expected occurrences
in the
dataset are counted. The counts from multiple sequences are averaged and
rounded down. The number of expected occurrences ![]() of a particular
pattern for a domain type is calculated as follows:
of a particular
pattern for a domain type is calculated as follows:
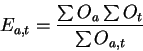 |
(2) |
When different patterns are compared with each other according to their
![]() deviations across multiple folding types a further adjustment is
required. To illustrate this, consider the 20 amino acids distributed
between three folding types A, B and C. We rank the amino acids by their
individual
deviations across multiple folding types a further adjustment is
required. To illustrate this, consider the 20 amino acids distributed
between three folding types A, B and C. We rank the amino acids by their
individual ![]() sums across the three types. Each
sums across the three types. Each ![]() score has 2
degrees of freedom, and we may find that proline has the highest
score has 2
degrees of freedom, and we may find that proline has the highest ![]() of 6.0. This is significant at the 95% level, i.e. 1 in 20
of 6.0. This is significant at the 95% level, i.e. 1 in 20 ![]() values of this magnitude will have occurred by chance (also written as
values of this magnitude will have occurred by chance (also written as
![]() ). Remember that there are 20 amino acids, so in effect we have
performed 20 experiments. Therefore the result for proline could easily
have arisen by chance.
). Remember that there are 20 amino acids, so in effect we have
performed 20 experiments. Therefore the result for proline could easily
have arisen by chance. ![]() must be adjusted in accordance with the number
of `replicates',
must be adjusted in accordance with the number
of `replicates', ![]() as follows[Martin et al.,
1995]:
as follows[Martin et al.,
1995]:
Estimates of statistical significance are not the primary concern of this
work. The ![]() analysis is used mainly to rank the likely contributions
of each pattern to the prediction accuracy.
analysis is used mainly to rank the likely contributions
of each pattern to the prediction accuracy. ![]() values resulting from
the analysis of sequence pattern frequency between different classes or
architectures (as described above) will be referred to as
values resulting from
the analysis of sequence pattern frequency between different classes or
architectures (as described above) will be referred to as ![]() (`t'
for type). In addition, we calculate
(`t'
for type). In addition, we calculate
![]() for each pattern
and fold type combination to determine which patterns are over and
under-represented in each folding type. It does not make sense to divide
this difference by
for each pattern
and fold type combination to determine which patterns are over and
under-represented in each folding type. It does not make sense to divide
this difference by ![]() because the prediction algorithm does not
currently use normalised pattern compositions.
because the prediction algorithm does not
currently use normalised pattern compositions.