advertisement: compare things at compare-stuff.com!

Three classes: mainly-$\alpha$, mainly-$\beta$ and mixed-$\alpha \beta$

We have looked at the single amino acid and duplet patterns in the three main classes. Tables 3.4 and 3.5 show these results in detail. Leu, Ala, Glu and Arg are both over-abundant in mainly-$\alpha$ domains and have significant $\chi _t^2$ at $P'<0.001$. Similarly for the mainly-$\beta$ domains, Thr, Cys, Gly, Ser, Asn, and Val are found more often than expected. The amino acids favoured by mixed-$\alpha \beta$ domains form an intersection between these two sets. Nakashima et al.nakashima:cpred reported similar trends in amino acid composition between mainly-$\beta$ proteins and mainly-$\alpha$ proteins. In their work, however, Lys, Met and His are favoured in $\alpha$-proteins, whilst in this statistical study concerning three classes, they are not found to be important. Differences due to dataset size and protocol may account for these anomalies, so they are not dwelled upon.

Comparison with the Chou and Fasmanchou:fasman propensities is also interesting. Leu, Ala and Glu are the three strongest helix formers according to Chou and Fasman, whilst Arg, which we find to vary significantly between the three classes, is `indifferent'. Only Val, Cys and Thr are Chou-Fasman strand-formers. Ser and Asn are weak strand-breakers, yet are over-abundant in mainly-$\beta$ proteins in our study. The apparent paradox here is quickly resolved when one considers that mainly-$\alpha$ and mainly-$\beta$ proteins are not entirely helix and sheet respectively; they have turns and loops which connect the secondary structures. Gly is commonly found in turns and other loops where it allows specific conformations to be attained (owing to the absence of a side-chain). In such a role it may be important in mainly-$\beta$ proteins. More discussion of this hypothesis will follow.

Table 3.4: Chi-squared analysis of amino acid usage between the three main classes. Values of $\chi_t^2>20$ are significant at the level of $P'<0.001$. Positive $O-E$ values are shown in bold (overabundant). In this and following tables, all patterns with significant $\chi _t^2$, or the top 10 are shown (whichever is the greater).

		Observed - Expected ($O-E$)
pattern	$\chi _t^2$	Mainly Beta	Alpha Beta	Mainly Alpha
T	92.5	280.6	-213.0	-67.5
L	89.2	-301.7	117.8	183.9
A	68.8	-286.6	193.4	93.1
C	67.1	119.5	-105.2	-14.2
E	64.6	-228.7	126.1	102.5
G	61.9	176.6	33.2	-209.8
S	60.7	233.7	-170.0	-63.7
N	39.6	163.0	-140.4	-22.5
V	34.2	84.2	75.1	-159.4
R	33.8	-129.3	35.2	94.0

Table 3.5: Chi-squared analysis of (i,i+3) duplet usage between the three main classes. Values of $\chi_t^2>26$ are significant at the level of $P'<0.001$.

			Observed - Expected ($O-E$)
pattern		$\chi _t^2$	Mainly Beta	Alpha Beta	Mainly Alpha
L	. .	L	60.0	-60.7	19.4	41.3
C	. .	G	43.3	17.1	-13.9	-3.2
A	. .	L	40.9	-52.9	30.7	22.2
K	. .	E	32.0	-12.5	-13.8	26.3
E	. .	K	31.5	-30.8	13.4	17.4
A	. .	E	31.5	-33.1	16.8	16.3
L	. .	A	31.4	-47.8	31.8	15.9
A	. .	A	29.4	-50.8	32.8	17.9
T	. .	S	28.5	28.7	-23.2	-5.4
C	. .	S	27.8	11.6	-9.1	-2.4
E	. .	R	26.6	-21.6	2.6	18.9

Since class predictions using (i,i+3) duplet composition perform better than those using amino acid composition, it is not surprising that their compositional differences (see Table 3.5) are also interesting. Pairs of helix-preferring residues predominate in both the helix-containing classes, as might be expected: Leu-X-X-Leu, Ala-X-X-Leu, Ala-X-X-Glu, Leu-X-X-Ala and Ala-X-X-Ala. However, Lys-X-X-Glu and Glu-X-X-Lys also exhibit significant $\chi _t^2$ across the three classes. Lys is only a weak helix former on the Chou-Fasman scale. Intriguingly, the Lys-X-X-Glu duplet is over-abundant only in mainly-$\alpha$ domains while the Glu-X-X-Lys duplet is over-abundant in both helix-containing classes. This will be discussed further below. Mainly-$\beta$ domains possess more Cys-X-X-Gly, Thr-X-X-Ser and Cys-X-X-Ser pairs.

Figure 3.4: Location of significant sequence patterns in protein structures. Red indicates overabundance of patterns for the class of domain shown. Blue indicates underabundance. (a) and (b): domain 1gmfA0. In (a) the amino acids with significant $\chi_t^2>20$ are coloured, whilst in (b) (i,i+3) duplets with $\chi_t^2>26$ are shown in colour. (c) domain 1pho00 shows patterns with $\chi_t^2>13$ for the barrel architecture (compared with sandwich and distorted sandwich architectures).

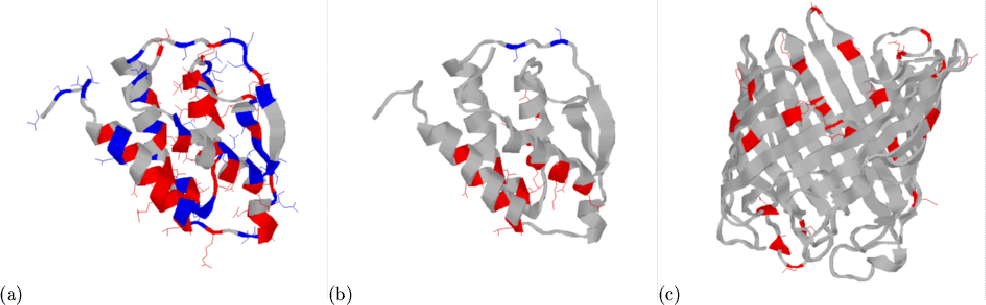We have attempted to give structural explanations for these observations, by highlighting occurrences of these patterns on 3D rendered structures (Figure 3.4). Unfortunately, the large number of structures has prohibited a comprehensive visual examination of the data. In Figure 3.4(a), the over- and under-abundant amino acids for mainly-$\alpha$ domains (from Table 3.4) are shown in red and blue respectively on the structure of granulocyte-macrophage colony-stimulating factor[Diederichs et al., 1991], domain 1gmfA0 in CATH. In part (b) of the figure, the same is shown for (i,i+3) duplets (from Table 3.5). The over-abundant duplets are clearly located in helices. The clearer distinction (more red than blue) in (b) compared with (a) is expected since duplets contain much more local structural information. An inspection of structures containing numerous Lys-X-X-Glu and Glu-X-X-Lys pairs showed that the majority of these do not form salt bridges, even though most are situated on the solvent accessible face of helices where their side-chains can be in close proximity.

$\chi_d^2$ analysis on the domains used in Table 3.5 showed many (i,i+3) patterns with structural preferences: the strongest preferences are for Pro- or Gly-containing patterns in loop or turn structures (data not shown). The patterns with class preferences (see Table 3.5) gave lower $\chi_d^2$ scores, but these were still significant ($d>>3$). These results confirm that the `helix' patterns discussed above (Leu-X-X-Leu, Ala-X-X-Leu, etc.) are over-abundant in helix.

The patterns with preferences for mainly-$\beta$ domains are more interesting. Cys-X-X-Gly has significant ($d>>3$) structural preferences and is over-abundant in turns. Cys-X-X-Ser is also over-abundant in turns, but its overall distribution is not significant ($d<0$). Thr-X-X-Ser is over-abundant in loops; its overall distribution is not very significant ($d=2.2$, $P=0.01$). The interesting observation here is that these patterns are not strand specific, although many patterns do have strand preferences (for example Gly-X-X-Ile and Val-X-X-Val). The majority of the information used in the three class prediction is helix-related (which explains the better quality predictions for mainly-$\beta$ domains).