Self-organising maps of two superfolds

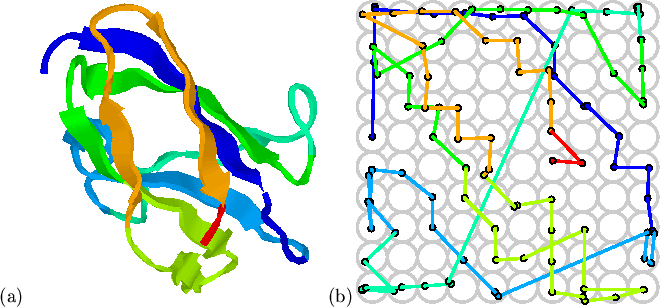
Figure 5.2 shows results of the mapping of the 107 carbon- $\alpha$ coordinates of domain 4 of cyclodextrin glycosyltransferase[Klein & Schulz, 1991, PDB entry 1cgt, CATH entry 1cgt04]. The largely non-overlapping chain trace through the map (Figure 5.2(b)) retains the ordering of most of the strands in this immunoglobulin-like fold. The two halves of the $\beta$ -sandwich occupy separate parts of the map. One major discontinuity (in green) occurs between residues 43 and 44 (sequential numbering starting from 1) where the chain crosses from one sheet to the other, and local distance constraints cannot be maintained.

**Figure 5.2:** Kohonen mapping of the three-dimensional carbon- $\alpha$ coordinates of domain 1cgt04. Map dimensions $10 \times 10$ (total 100 units). (a) cartoon representation of 1cgt04 produced using Rasmol[Sayle & Milnerwhite, 1995] in an arbitrary view to show the similarity between structure and mapping. (b) Trajectory of the carbon- $\alpha$ trace in the Kohonen map (see Section 5.2.2 for a description of this representation). Most inter-strand relationships are preserved. A major discontinuity can be seen in this representation as the green line linking the top and bottom rows of the map; this is where local relationships have been sacrificed in favour of the consistency of the rest of the map. The colouring scheme is identical in (a) and (b) - the N-terminus is shown in blue and the C-terminus in red.
$\begin{figure}\begin{center} \par (a)~\epsfig{file=chap5/figs/struct/1cgt04.ps,w... ...e=chap5/figs/struct/1cgt04_tr.eps,width=\twotoapage}\par\end{center}\end{figure}$

**Figure 5.3:** Kohonen mapping of the three-dimensional carbon- $\alpha$ coordinates of domain 1ghsA0. Map dimensions $17 \times 17$ (total 289 units). see Figure 5.2 for description of (a) and (b). The central $\beta$ -barrel of this TIM-barrel is preserved in the map.
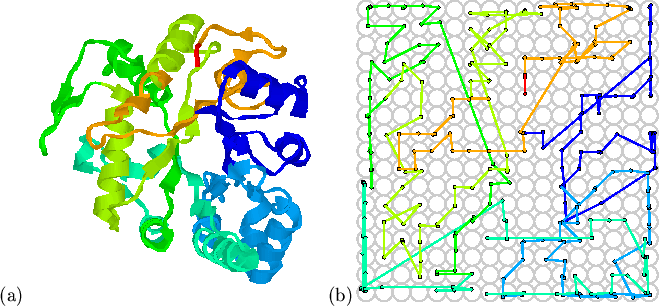$\begin{figure}\begin{center} \par (a)~\epsfig{file=chap5/figs/struct/1ghsA0.ps,w... ...e=chap5/figs/struct/1ghsA0_tr.eps,width=\twotoapage}\par\end{center}\end{figure}$

Figure 5.3 shows the mapping of a larger protein domain; 1ghsA0[Varghese et al., 1994] from the CATH database; this 1,3- $\beta$ -glucanase is a TIM-barrel domain[Farber, 1993,Orengo et al., 1994,Reardon & Farber, 1995] consisting of an 8-fold repeat of a basic $\beta\alpha\beta$ super-secondary motif. As in Figure 5.2, the major relationships have been preserved: the central $\beta$ -barrel and the arrangement of the surrounding helices. The mapping is more complex than the previous immunoglobulin-like example, and the preservation of important contacts is not obvious without detailed inspection.

The intramolecular distance matrix[Phillips, 1970] is a representation of protein structure which allows all contacts to be visualised simultaneously. The top half of Figure 5.4 shows a Euclidean distance matrix, calculated from the input data (carbon- $\alpha$ coordinates). The amino-terminus of the sequence is located at the bottom left corner. White regions indicate residue pairs in close contact (the grey-scale is normalised to white=closest distance, black=furthest distance). The bottom half shows the Euclidean distances for the same residue pairs calculated from the map coordinates (hence the distance between residue A mapping to $r_{2,2}$ and residue B mapping to $r_{5,6}$ would be $\sqrt{3^2+4^2} = 5$ ). The two matrices share the same major features: the clear pattern of parallel $\beta$ -strands and helices in the first third of the sequence in particular. The correlation coefficient between the real distances and the map distances is 0.85.